3月16日上午，“统计大讲堂”系列讲座第186讲举行。本次讲座采取线上会议的方式，邀请南方科技大学数学系助理教授张艺赢作题为“基于非齐次风险的满意信度理论方法”的报告。讲座由中国人民大学统计学院副教授、应用统计科学研究中心研究员高光远主持。

高光远首先介绍了主讲人的相关信息。张艺赢是南方科技大学数学系助理教授、博士生导师，于2012年及2015年分别在兰州大学数学与统计学院获得理学学士和硕士学位，于2018年9月在香港大学统计与精算学系获得精算学方向哲学博士学位。目前的主要研究领域包括风险管理与保险精算、应用概率及可靠性理论与统计。主要研究兴趣包括最优再保险、信度理论、系统性风险、风险测度、相依风险模型、随机序理论及随机比较、可靠性分析及系统可靠性设计与优化。已在保险精算主要期刊IME、SAJ、ASTIN Bulletin和NAAJ，以及运筹管理领域主流期刊EJOR、RESS和NRL等杂志发表多篇学术研究论文。

张艺赢首先简单阐述了信度理论并介绍了其百年来的具体发展历程。该理论常被应用于保险领域，能够从保险公司的角度出发，把个人和整体的信息进行融合，从而解决合理增收保费的问题。根据已知信息的不同，学者将增收保费分为个体溢价、集体溢价和贝叶斯溢价三种方法，其中贝叶斯溢价效果最好。

虽然贝叶斯框架在理论上十分完善，但是实际应用时的效果受后验概率选取的影响较大，所以Bühlmann提出了一种逼近个体溢价的优化方法，构造了Simple Bühlmann Model。在详细解释该模型的原理后，张艺赢介绍了近十年内以Simple Bühlmann Model为基础，对目标函数进行改变的研究成果。同时，他指出该模型对异常值有高度敏感性，所以稳健性较低。

为了解决上述缺点，De Vylder首先提出对观测值进行截断形式的数据转换的方法，Gisler后来也进一步指出，L2最优截断点的选取可以通过一种特殊的方式确定，但其显式公式的推导十分困难，而且并未推广至半连续数据和连续数据上，这也是张艺赢所在团队的研究背景。

在阐述了前人研究成果之后，张艺赢指出所在团队的研究借助正规变化函数对随机变量X的尾部函数特征进行刻画和建模。在进行建模时需要借助Fisher-Tippet 理论，如果确定X的极值分布属于Frechet、Gumbel、Weibull分布的其中一种，则称X属于某一类极值分布的系数域，从而简化分析过程。

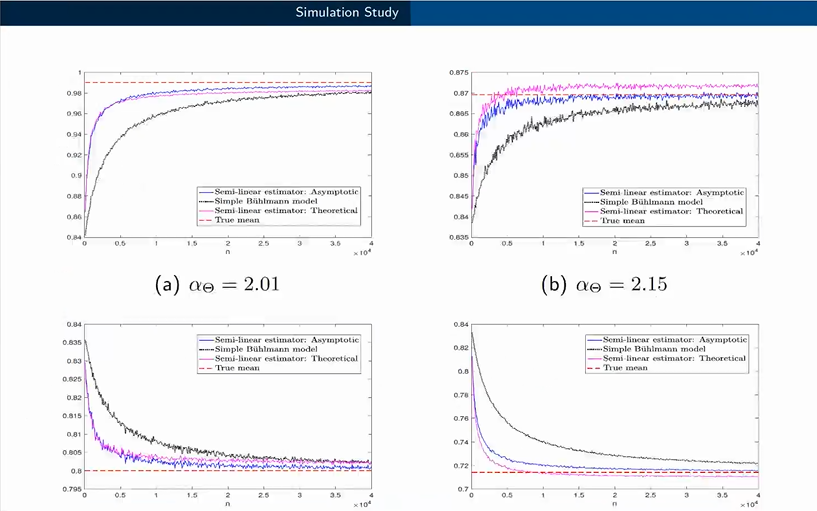
紧接着，张艺赢介绍了研究团队构建的模型，为了在实际使用和数学可处理性之间取得平衡，他们重点关注来自不同的极值分布MDA的异构风险，并结合运筹学的方法，通过提供最佳截断点的显式公式来缩小差距，直至得到渐进意义上最优的函数。张艺赢通过图示向同学们生动地展示了逼近过程。一项全面的数值研究表明，借助这个新得到的截断点，相应的半线性可信度公式优于经典的Bühlmann模型。

最后，在提问交流环节，在线师生积极参与讨论，张艺赢耐心解答了同学们的疑问，就半线性信度估计问题做了更加深入的探讨。