6月28日上午，“统计大讲堂”系列讲座第195讲举行。本次讲座采取线上会议的方式，邀请香港大学教授李国栋作题为“一种高效的高维数据张量回归方法”的报告。讲座由应用统计科学研究中心研究员、中国人民大学统计学院教授许王莉主持。

许王莉首先介绍了主讲人的相关信息。李国栋于北京大学获得了统计学学士和硕士学位。2007年，获得香港大学统计学博士学位，随后在新加坡南洋理工大学数学科学系担任助理教授。2009年，加入香港大学统计与精算系担任助理教授，现任教授。

李国栋首先介绍了有关张量的背景知识。他通过具体的例子，指出在当下社会，随着数据数量的增多和结构的复杂化，张量的应用愈发普及。而这种实用价值正是激励他们开展研究的动力之一。随后，他介绍了Tensor regression和Tensor autoregression的相关内容，并指出当使用此类回归的时候，参数个数膨胀非常快。为解决这一问题，需进行系数降维和张量分解。

接下来，李国栋着重介绍了张量分解所使用的工具。他给出了矩阵化的定义，即将一个张量压缩成平板的矩阵。常用的矩阵化方法有两种——one-mode matricization和sequential matricization。他对这两种方法进行了详细讲解，并根据公式指出二者的区别。

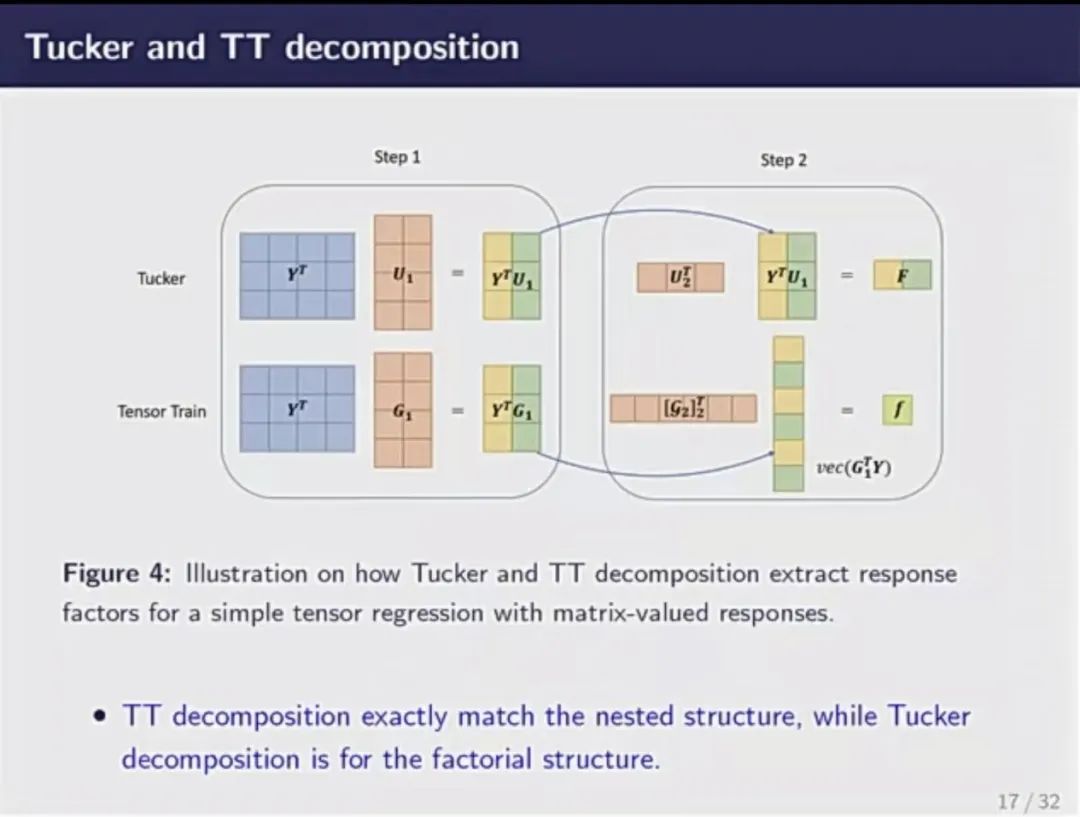
随后，他介绍了张量的三种分解方式——CP分解、Tucker分解和TT分解。CP分解对张量压缩程度最大，故可以处理更高阶的张量。但它缺乏理论性质，且优化非常不稳定。Tucker分解与one-mode matricization对应，基本思想为，一个大立方体可通过一个小立方体在三个方向上扩张得到。它是目前最常用的分解方式，优化性质非常稳定。但由于过于谨慎，压缩速度慢，需要消耗的参数非常大。TT分解则是综合了上述两种方法的优点，性质稳定、压缩速度快。然而，它缺乏可解释性，故未能在学界流行。李国栋及其团队在前人研究的基础上，引入正交性，对TT分解做出了合理的解释，保证其可以应用到回归当中。

基于上述对张量分解的讨论，李国栋介绍了Tucker分解和TT分解应用至tensor regression中的具体方式。并且，通过对比两种应用方式，他指出了两种分解方法的区别，一是参数个数不同，二是压缩参数的方式不同。TT分解的参数个数更少，压缩方式更简洁，具有灵活性。随后，他通过数学公式讲解了TT regression的思想，介绍了如何安排响应和预测，并呈现了模拟实验的结果。

在提问交流环节中，在线师生就所讲内容积极提出问题，李国栋耐心清楚地解答了大家的疑问，并对TT分解的改进过程作了进一步的阐释。